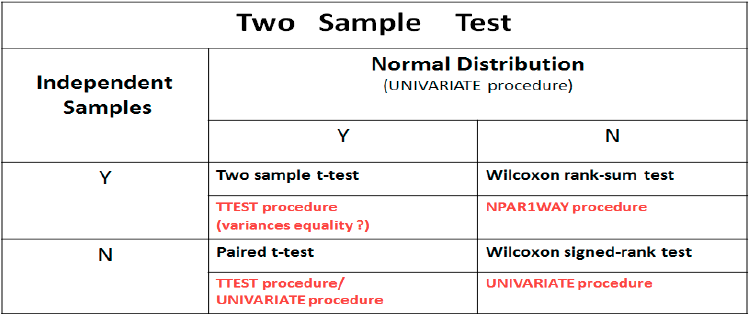
In clinical trial, two-sample hypothesis testing is usually applied when testing if there is a difference between two means from two different populations receiving different treatments like placebo treatment and drug treatment. Generally speaking, there are four statistical methods that can be used for two sample test: two sample t-test, Wilcoxon rank-sum test, paired t-test and Wilcoxon signed-rank test. Before applying a statistical test, we need to check that the assumptions of this test are not violated.
Here is a summary of the assumptions and corresponding statistical test. If the two samples are independent and both of them are normally distributed, two sample t-test will be used. Wilcoxon rank-sum test should be applied if the two samples are independent and not normally distributed (even if only one is not normally distributed). Paired t-test will be used if they are normally distributed but are not independent. And the last one – Wilcoxon signed-rank test – should be applied when both of these two assumptions are violated. The normality can be tested using SAS. As for the assumption about independent or not, we have to make a decision based on the study design. In the following table, I also listed corresponding SAS procedure (in red) for each kind of test. For example, PROC TTEST can be used for two sample t-test while PROC NPAR1WAY can be used for Wilcoxon rank-sum test.
Check the Assumption of Normality
PROC UNIVARIATE can be used to test for normality. By applying NORMAL option in PROC UNIVARIATE statement, SAS can provides you test statistics and p-values for the Shapiro-Wilk test, the Kolmogorov-Smirnov (K-S) test, the Anderson-Darling test, and the Cramér–von Mises test. You can see the statistics and p-values in the output NORMAL_CHK dataset. Shapiro-Wilk test and the Kolmogorov-Smirnov (K-S) test are more popular of them. Shapiro-Wilk test is preferable when the sample size is less than or equal to 2000 while Kolmogorov-Smirnov (K-S) test is recommended provided the sample size is over 2000. The sample size is stored in OBS_NUM dataset. By merging NORMAL_CHK and OBS_NUM, we can use IF statement to keep correct statistical test and corresponding result. Both of these two tests test the hypothesis that if the distribution is normal. Therefore, If p-value is greater than 0.05, we consider that the sample is normally distributed. Otherwise, the sample is not normally distributed.
Following is the macro to test normality and how to use test normality of variable HEIGHT in SASHELP.CLASS using this macro. By running below code, we can get that HEIGHT is normally distributed for both female and male group.
Click here to hide/show code
%macro normal_chk(data=, var= , grp = );
proc sort data = &data out = temp; by &grp; run;
data temp;
set temp;
by &grp;
if first.&grp then n +1;
run;
proc sort data = temp; by n &grp; run;
ods listing close;
ods output TestsForNormality = normal_chk Moments = obs_num;
proc univariate data = temp normal;
by n &grp;
var &var;
quit;
ods output close;
ods listing;
proc sql;
create table f_normal_chk as select a.n, a.&grp,cValue1,Test,
pvalue from obs_num(where = ( trim(label1) = “N”)) as a inner join Normal_chk as b on a.&grp = b.&grp;
quit;
data f_normal_chk;
set f_normal_chk;
if (cvalue1 >=2000 and test = “Kolmogorov-Smirnov”) or /* sample size is over 2000, the Kolmgorov test*/
(cvalue1 < 2000 and test = “Shapiro-Wilk”); /*sample size is less than 2000, the Shapiro test */ if pvalue > 0.05 then
norm = “Y”;
else norm = “N”;
run;
proc sql;
create table norm_chk as select a.norm as normal1, b.norm as normal2 from
f_normal_chk(where= ( n = 1)) as a ,f_normal_chk(where= ( n = 2)) as b;
quit;
%mend;
%normal_chk(data=sashelp.class, var= height, grp = sex);
Two sample t-test
PROC TTEST can be applied for two sample t-test. Here we also have to check if the variance is equal between two samples. It tests whether the variances are equal for both two groups. Thus we can get a conclusion that the variances are equal if PROBF in EQUALITY dataset is greater than 0.05. In the TTEST dataset, SAS also gives us three methods to test if the means are equal between two groups. Pooled and Satterthwaite are used in most cases. Pooled assumes that variances are equal while Satterwaite assumes unequal variances. Here is how to test if the mean of height are equal for female and male groups.
Click here to hide/show code
%macro ttest(data=, var= , grp =);
ods listing close;
ods output Equality = equality TTests = TTest;
proc ttest data = &data;
class &grp;
var &var;
run;
ods output close;
ods listing;
proc sql;
create table f_ttest as select a.fvalue, a.probF, b.Method,b.Variances,b.tvalue,b.probt from equality as a , ttest as b;
quit;
data f_ttest;
length method $40.;
set f_ttest;
if (probF > 0.05 and trim(left(method))= “Pooled”) or /*variances are equal*/
(probF <=0.05 and trim(left(method)) = “Satterthwaite”); /*variances are not equal*/
pvalue = put(probt,pvalue8.3);
Method = ‘Two sample t Test’;
if probt < 0.05 then
Significant = ‘Y’;
else Significant = ‘N’;
run;
proc sql;
create table comp as select method, pvalue, significant from f_ttest;
quit;
%mend;
%ttest(data=sashelp.class, var= height, grp =sex);
Wilcoxon rank-sum test
Wicoxon rank-sum test (also called the Mann-Whitney-Wilcoxon (MWW), Mann-Whitney U test, Wilcoxon-Mann-Whitney test) is a nonparametirc test. The null hypothesis is that it is equally likely that a randomly selected value from one sample wil be less then or greater than a randomly selected value from another sample. And thus we will get a conclusion that the value between two samples are significantly different if two sided p-value is less than 0.05. Here I have to remind that when the sample size is small, WILCOXON option in the EXACT statement should be used and it can get you the exact p-values for the Wicoxon test.
Click here to hide/show code
%macro wmut(data=,var=,grp=);
ods listing close;
ods output WilcoxonTest = WMWtest;
proc npar1way data = &data wilcoxon;
class &grp;
var &var;
exact wilcoxon;
run;
ods output close;
ods listing;
data Wmwtest_;
length method $40.;
set Wmwtest;
if trim(left(name1)) = “XP2_WIL”;
pvalue = put(nvalue1,pvalue8.3);
Method = ‘Wilcoxon Rank-sum Test’;
if nvalue1 < 0.05 then
Significant = ‘Y’;
else Significant = ‘N’;
run;
proc sql;
create table comp as select method, pvalue, significant from Wmwtest_;
quit;
%mend;
Paired t-test
Paired t-test is also a parametric test and it is also known as Dependent t-test. It determines whether there is a statistical evidence that the mean difference between paired observations is significantly different from 0. If p-value is less than 0.05, we consider that the mean difference is sinificantly different from 0.
Click here to hide/show code
%macro p_ttest(data=, var1= , var2 =);
ods listing close;
ods output TTests = TTest;
proc ttest data = &data;
paired &var1*&var2;
run;
ods output close;
ods listing;
data ttest;
length method $40.;
set ttest;
pvalue = put(probt,pvalue8.3);
Method = ‘Paired t Test’;
if probt < 0.05 then
Significant = ‘Y’;
else Significant = ‘N’;
run;
proc sql;
create table comp as select method, pvalue, significant from ttest;
quit;
%mend;
Wilcoxon signed-rank test
Wilcoxon signed rank test is non-parametric test which does not require the data to be normally distribute. However, we have to create a new variable which can store differences betwee the paired observations.
Click here to hide/show code
%macro wsrt(data=, diff=);
ods listing close;
ods output TestsForLocation = wsrt;
proc univariate data = &data;
var &diff;
run;
ods output close;
ods listing;
data wsrt;
length method $40.;
set wsrt;
if trim(left(test)) = “Signed Rank”;
pvalue = put(pvalue,pvalue8.3);
Method = ‘Wilcoxon Signed Rank test’;
if pvalue < 0.05 then
Significant = ‘Y’;
else Significant = ‘N’;
run;
proc sql;
create table comp as select method, pvalue, significant from wsrt;
quit;
%mend;
Summary
With above five macros, here I create a new macro which can choose the right methods and compute p-values automatically. At first, we need to call macro NORMAL_CHK to test the normality. With the macro variable INDEP, we can use IF statement to call for different macros. For example, if value of INDEP is N and the result returned from NORMAL_CHK is Y for both two groups, a two sample t-test and thus TTEST macro will be used.
Click here to hide/show code
%macro comp_p(indep= , data =, var = , grp = , var1 = , var2 =, diff = ) ;
****set a macro variable to indicate whether the two samples are independent or not;
data indep;
indep = “&indep”;
run;
**** *Check assumption and Compute pvalue **********************************;
data _null_;
call execute(‘%normal_chk(data= &data, var=&var , grp = &grp)’);
run;
proc sql;
create table asump_chk as select * from indep, norm_chk;
quit;
data _null_;
set asump_chk;
if Indep = “Y” then
do;
if Normal1 = “Y” and Normal2 = “Y” then
call execute(‘%ttest(data= &data, var=&var , grp = &grp)’);
else call execute(‘%wmut(data= &data,var=&var,grp = &grp)’);
end;
else if Indep = “N” then
do;
if Normal1 = “Y” and Normal2 = “Y” then
call execute(‘%p_ttest(data= &data, var1=&var1 , var2 = &var2)’);
else call execute(‘%wrst(data= &data, diff=&diff)’);
end;
run;
%mend;